功利的进步——阿姆达尔定率
昨天阅读了闭环回路反思了对自己的启发之后,在解决方案2里面提到了更功利的学习,即优先学习对自己目前第一目标有用的东西。阿姆达尔定率是上个世纪IBM的大型机 System360 之父提出来的,System360是世界上最成功的大型机(没有之一),阿姆达尔博士在设计它时充分认识到了计算机各部分的性能必须平衡匹配,才能达到整体性能的最佳。他的思想通过一个很简洁的共识就可以表达出来。
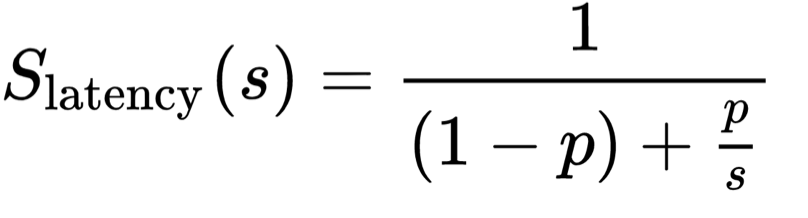
这个公式很简单,小学数学就能看懂,公式的各个部分含义如下
左边的S:整体系统性能的提升
右边的P:某一项性能指标占用系统整体运行时间的耗时
右边的S:某一项性能指标提升
例如,内存占用了整体系统性能耗时的20%记为 0.2 ,那么此次将内存的性能提升为原来的200% 记为2,最终系统性能整体提升 1.111 = 1 /((1 – 0.2) + (0.2 / 2)) ,性能提升了大约 11% ,但是如果把性能提升1000%,最终结果是整体性能提升了25%,付出了多10倍的性能提升最后只换来了整体提升的幅度多一倍,可能就有点得不偿失了。
这个定律成为了IT行业发展的战术指导思想,每次在设计新一代的计算机产品时各个细分行业的新技术有很多,而用于改进的资金和时间资源也是有限的,因此只能优先改进对于整个系统性能提升最大的部分。不仅仅是计算机设计时阿姆达尔法则是铁律,在软件开发调试软件性能时,负责任的工程师都会将各个模块进行优化,通过profile工具获悉到每个模块资源占用的情况,从最占用系统资源和最容易改进的地方入手,很容易将性能大幅提高。
阿姆达尔定律对于计算机行业是如此的重要, 有人甚至说凡是从事计算机工作的人都应该把阿姆达尔定律放在脑子最容易想到的地方,以此为行动准则,这是计算机行业快速进步的原因。
那么回到主线问题来,对于功利的进步,通过阿姆达尔定率有哪些启发呢?
可能有人会说,这个定律很笨啊,因为大家都是这样在做的呀,要改进当然要优先考虑问题的大头,说和不说有什么区别?但是做起来可真就不是那样了。
1、特长和喜好偏误干扰
比如有的公司的工程主管,做了一辈子的存储就永远强调存储的重要性,做处理器的主管也是强调他那部分的重要性,没有原则的公司要么在各个方向上面面俱到,要么就是在做对于主要目标没有必要的投入,很快就会落后。据说建三峡大坝水电站的时候也是如此,火电、核电等专家都去帮水电专家分析问题,证明三峡大坝是如何不好。原因也很简单,三峡大坝是当时的一个巨无霸工程,如果开始修建,那么较长一段时间内资源都会倾斜给水电,其他兄弟行业就没得捞了。
对于个人也是一样,在1+1的时候可以简明清晰的回答出问题,但是在决策情况稍复杂一些后,动作变形就来了,在投资和学习中尤为常见,而阿姆达尔面对的计算机系统就是一个非常复杂的问题。要想最快达到目标就必须抛开各种干扰因素,直击问题的本质,如何抛开干扰客观理性的思考呢,一个重要指标就是是否可量化。
2、是否清晰可量化、可操作
阿姆达尔的一个伟大之处在于他把这个问题量化为了一个简单的公式,使用者可以利用这个公式来快速的衡量改进是否合理。
人经常会陷入自己给自己挖的坑,例如我要完成A,但是又需要学习B,学习B好像还要C … 进入了一个递归循环中,最后没有原则的做了一堆“看似有用”的事情,精力都这样被耗散在了里面,而要完成的主要目标恐怕都忘了。
首先明确自己的长期目标是什么,一定要清晰明了(诸如阿姆达尔的目标就是提升系统性能),然后目标分解,画一张图,图里面标注完成目标的每个要素,依据完成要素的难度和对目标的贡献值进行优先级排序,每个阶段重点完成一个最“功利”的目标。下一个阶段再次按照相同的方式评估,再完成一个最“功利”的目标。循环几个阶段之后,总结出自己的阿姆达尔定律。另外阶段目标可以使用OKR进行管理和量化。
如果目标太大,分解之后还是挺大的怎么办?这说明目标设定的不够好,可以采用分而治之,分解为多个大目标,然后选取各个大目标的最高优先级子目标在下一个周期并行处理。注意不是所有的都可以并行处理,比如学习算法和跑步是可以的,但是既要学好算法又要学好英语之类的目标可能难以同时做到(依据时间而定),避免同类目标,如果需要分解的大目标太多则说明需要减少目标。
部分内容摘自——吴军谷歌方法论 IT行业为什么进步这么快?